ADP 실기 실습 / 기출 문제 / 시계열 분석 / ARIMA

12월 13일에 있을 ADP 실기를 준비하기 위해,
우선은 인터넷상의 실기 후기들을 수집 중이다.
얼마 전 18회에 등장한 시계열 분석 기출문제를 참고하여 간단한 예제로 실습해보려 한다.
제 18회 ADP 기출문제
계절성 시계열 분석문제
(데이터구성 : Year/month/amount)
- 정상성 확인 (10점)
- ARIMA모델 3가지 제시 (10점)
- 한가지 모델을 최종 선택하고 이유를 서술 (15점)
- 최종 예측을 하고, 실제 결과와 비교 평가하고 그 평가 방법을 사용한 이유를 제시 (15점)
시계열 자료란?
시간의 흐름에 따라 관찰된 값들을 시계열 자료라 한다.
시계열 분석을 통해 미래의 값을 예측하고 경향, 주기, 계절성 등을 파악하여 활용한다.
시계열 분석을 위해서는 기본적으로 아래의 정상성(Stationary)를 만족해야 한다.
- 평균이 일정하다.
- 분산이 시점에 의존하지 않는다.
- 공분산은 단지 시차에만 의존하고, 시점 자체에는 의존하지 않는다.
위 3가지 조건 중 하나라도 만족하지 못한다면, 비정상 시계열이라고 부른다.
실제 현실의 시계열 데이터는 비정상 시계열이 대부분이며,
비정상성 시계열 자료는
1. 평균이 일정하지 않다면(추세가 존재) "차분(Difference)" 을 통해
2. 분산이 일정하지 않다면 "변환(Transformation)"을 통해
가공하여 정상 시계열 자료로 만들어 줘야한다.
R을 활용한 시계열 분석하기
R에서 시계열 분석을 하는 순서는 다음과 같다.
1) 시계열 자료를 시각화하여 정상성 시계열인지 확인한다.
2) 시계열 자료를 정상성 시계열로 변환한다.
3) ACF/PACF 차트나 auto.arima 함수를 사용하여 최적화된 파라미터를 찾는다.
4) ARIMA 모형을 만든다.
5) 미래 추이를 예측한다.
예제 실습
예제 데이터는 1946년 1월부터 1959년 12월까지 뉴욕의 월별 출생자수 데이터를 scan함수로 불러와 활용한다.
먼저, 시계열 분석을 위해서는 Time-Series 객체가 필요하다.
숫자를 담고 있는 벡터를 Time-Series 객체로 변환하려면 ts (대상 벡터) 함수를 사용하면 된다.
install.packages("TTR")
install.packages("forecast")
install.packages("tseries")
library(TTR)
library(forecast)
library(tseries)
data <- scan("http://robjhyndman.com/tsdldata/data/nybirths.dat")
birth <- ts(data, frequency = 12, start = c(1946, 1)) #숫자벡터를 Time-Series 객체로 변환
1) 데이터 정상성 확인
시계열 자료를 plot 명령어로 시각화하여 정상성 시계열인지 간단히 확인한다.
plot.ts(birth, main = "뉴욕 월별출생자 수")

시각화 결과, 시간에 따라 평균과 분산이 증가하는 경향이 있어 "뉴욕 월별출생자 수" 데이터 셋은 정상성 시계열이 아닌 것으로 판단된다. 참고로, decompose()함수를 사용하면 데이터셋을 4가지 요인으로 분해 시켜준다.
autoplot(decompose())를 사용하면 data / trend / seasonal / remainder 컬럼으로 나눠진 그래프를 확인할 수 있다.
autoplot(decompose(birth)) #시계열 데이터를 4가지 요인으로 분해한 후 도식화
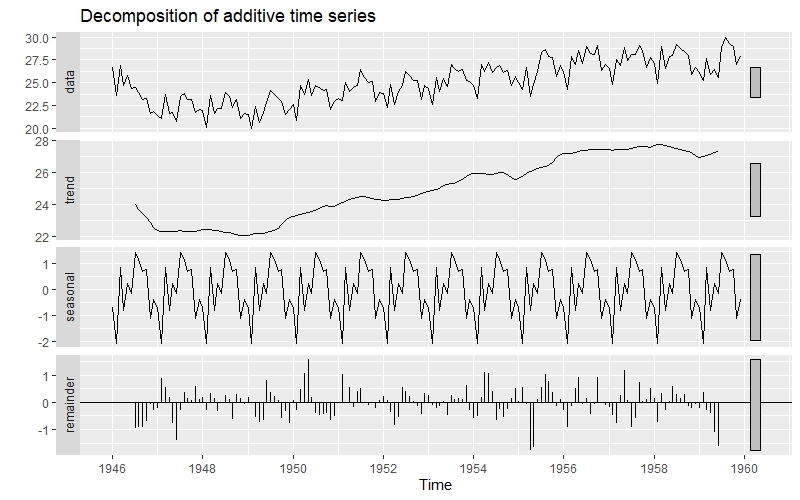
2) 정상성 시계열 자료로 변환
주어진 비정상성 시계열 데이터를 정상성 시계열로 바꾸는 방법은 두 가지가 있다.
(1) 차분(diff) : 평균이 일정하지 않은 시계열을 정상화하는 방법으로, 현 시점 자료에서 전 시점 자료를 빼는 것
- 일반차분(regular difference) : 바로 전 시점의 자료를 빼는 방법
- 계절차분(seasonal difference) : 여러 시점 전의 자료를 빼는 방법 (주로 계절성을 갖는 자료의 정상화에 사용)
- 함수 : diff(data, lag=k, diff=d) : 지연차수 k 및 차분차수 d의 차분을 수행 (k와d의 default값은 0)
(2) 로그변환(log) : 시계열 자료를 로그함수로 변환하여 정상화하는 방법으로, 반드시 "차분" 전에 진행되어야 한다.
위의 시계열 자료는 평균과 분산 둘다 비정상이므로 로그변환 후 차분한다.
tseries 패키지에 내장되어 있는 adf.test 함수로 시계열이 정상성 시계열인지 확인한다.
p-value가 0.01이므로 유의수준 0.05 하에서 로그변환 후 차분한 데이터셋은 정상성 시계열이라고 할 수 있다.
birth1 <- diff(log(birth))
adf.test(birth1, alternative="stationary", k=0)
Augmented Dickey-Fuller Test
data: diff(log(birth))
Dickey-Fuller = -23.589, Lag order = 0, p-value = 0.01
alternative hypothesis: stationary
3) ACF/PACF 차트나 auto.Arima 함수를 사용하여 최적화된 파라미터 찾기
(1) ACF
- lag는 0부터 값을 갖는데, 너무 많은 구간을 설정하면 그래프를 보고 판단하기 어렵다. (max=20으로 설정)
acf(birth1, lag.max=20) # 자기상관계수 그래프 출력

(2) pacf
pacf(birth1, lag.max=20) # 편자기상관계수 그래프 출력

acf 와 pacf의 lag 절단값이 명확하지 않아 Arima 모형 확정이 어려우므로, auto.arima 함수를 사용한다.
auto.arima(birth)
Series: birth
ARIMA(2,1,2)(1,1,1)[12]
Coefficients:
ar1 ar2 ma1 ma2 sar1 sma1
0.6539 -0.4540 -0.7255 0.2532 -0.2427 -0.8451
s.e. 0.3004 0.2429 0.3228 0.2879 0.0985 0.0995
sigma^2 estimated as 0.4076: log likelihood=-157.45
AIC=328.91 AICc=329.67 BIC=350.21
tsdiag(auto.arima(birth)) #자기상관함수에 의한 모형 진단(모형 타당성 검정)
아래의 그림은 auto.arima 함수를 사용해서 구한 파라미터가 모형의 가정을 만족하는지를 보여주는 그림이다.
- 첫번째 그래프를 보면 뚜렷한 증가 및 감소 패턴이 없음
- 두번째 잔차의 자기상관함수 그래프(ACF of Residuals)를 보면 모두 파란선(임계치) 안에 들어있으므로
자기상관관계가 없고, 규칙성이 보이지 않음
- 세번째 Box-Ljung 검정 그래프에서는 p-value값이 0이상으로 분포됨 (파란색 점선 : 유의확률 0.05)
위의 내용을 보면 ARIMA 모형이 양호한 시계열 모형을 보이며, 모델이 적합하다고 볼 수 있다.

4) Arima 모형 만들기
auto.arima에서 구한 파라미터로 ARIMA 모형을 만들어 본다.
아래 코드를 사용하여 ARIMA 모형을 만들고, 다음 단계에서 향후 2년간의 추이를 예측해보도록 한다.
birth_arima <- arima(birth, order = c(2,1,2), seasonal = list(order = c(1,1,1), period = 12))
birth_arima
Call:
arima(x = birth, order = c(2, 1, 2), seasonal = list(order = c(1, 1, 1), period = 12))
Coefficients:
ar1 ar2 ma1 ma2 sar1 sma1
0.6539 -0.4540 -0.7255 0.2532 -0.2427 -0.8451
s.e. 0.3004 0.2429 0.3228 0.2879 0.0985 0.0995
sigma^2 estimated as 0.3918: log likelihood = -157.45, aic = 328.91
5) 미래 추이에 대하여 예측하기
birth_fcast <- forecast(birth_arima, h=12*2) #12개월 주기로 향후 2년의 미래 추이를 예측, default값은 2년
birth_fcast
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 1960 27.69056 26.88679 28.49433 26.46130 28.91982
Feb 1960 26.07680 24.98034 27.17326 24.39991 27.75369
Mar 1960 29.26544 28.04020 30.49069 27.39160 31.13929
Apr 1960 27.59444 26.29165 28.89724 25.60199 29.58689
May 1960 28.93193 27.54860 30.31527 26.81630 31.04757
Jun 1960 28.55379 27.07347 30.03411 26.28983 30.81774
Jul 1960 29.84713 28.26538 31.42888 27.42806 32.26620
Aug 1960 29.45347 27.77916 31.12778 26.89284 32.01410
Sep 1960 29.16388 27.40777 30.91999 26.47814 31.84962
Oct 1960 29.21343 27.38167 31.04519 26.41200 32.01486
Nov 1960 27.26221 25.35695 29.16746 24.34837 30.17604
Dec 1960 28.06863 26.09098 30.04628 25.04408 31.09318
Jan 1961 27.66908 25.63754 29.70062 24.56210 30.77606
Feb 1961 26.21255 24.12791 28.29719 23.02437 29.40073
Mar 1961 29.22612 27.08633 31.36591 25.95360 32.49865
Apr 1961 27.58011 25.38474 29.77547 24.22259 30.93762
May 1961 28.71354 26.46431 30.96277 25.27363 32.15344
Jun 1961 28.21736 25.91651 30.51820 24.69852 31.73620
Jul 1961 29.98728 27.63644 32.33812 26.39198 33.58258
Aug 1961 29.96127 27.56138 32.36117 26.29095 33.63160
Sep 1961 29.56515 27.11690 32.01339 25.82088 33.30941
Oct 1961 29.54543 27.04965 32.04121 25.72846 33.36240
Nov 1961 27.57845 25.03603 30.12088 23.69015 31.46676
Dec 1961 28.40796 25.81976 30.99616 24.44965 32.36627
plot(birth_fcast, main = "Forecasts 1960~1961")

파란색 선 부분이 예측치이다. 계절성과 추세가 잘 반영된 예측 결과로 보인다.
지금까지 시계열 분석의 다양한 기법 중 가장 일반적으로 사용되는 ARIMA 모형에 대해 알아보았다.
최종 예측을 하고, 실제 결과와 비교 평가하는 방법에 대해서는 다음 포스팅에..
'Work > ADP' 카테고리의 다른 글
| [ADP 실기 준비] R 기계 학습 - 분류분석 모델링 및 성과 분석 (6) | 2020.10.30 |
|---|---|
| [ADP 실기 준비] R프로그래밍 기계 학습 - 탐색적 자료분석(EDA) (2) | 2020.10.28 |
| [ADP 실기 준비] R 프로그래밍 기계 학습 - 데이터 전처리 (8) | 2020.10.21 |
| [ADP 실기 준비] R 시계열 분석 2탄 / ARIMA 모델 / 기출공략 (0) | 2020.10.14 |
| 제 18회 ADP(데이터분석 전문가) 필기/독학/합격 후기 (83) | 2020.10.09 |




댓글