[ADP 실기 기출 공략] R 프로그래밍 기계 학습 / 파생 변수 추가 /모델 설계 및 학습 / 의사결정 나무 / 랜덤 포레스트
이번에는 데이터 탐색 및 시각화에 이어 파생변수 추가와 모델 설계 및 학습 과정에 대하여 알아볼 것이다.
데이터 분석 시, 주어진 데이터를 그대로 사용하지 않고 분석 목적에 맞게 데이터 형태를 변환하여 사용하는 경우가 많다.
이렇게 파생변수를 추가한 후, 최종적으로 모델을 설계하고 기계 학습시키는 방법에 대하여 살펴보자.
예제 데이터는 지난번에 사용하던 titanic 데이터를 그대로 사용한다.
2020/10/28 - [데이터분석 with R/ADP] - [ADP 실기 준비] R프로그래밍 기계 학습 - 탐색적 자료분석(EDA)
[ADP 실기 준비] R프로그래밍 기계 학습 - 탐색적 자료분석(EDA)
[ADP 실기 기출 공략] R 프로그래밍 기계 학습 / 탐색적 자료 분석(EDA) / 데이터 시각화 지난 포스팅에서 기계 학습을 위한 데이터 전처리 과정 중, 데이터 타입 변환, 결측치 확인 및 처리에 대해서
ckmoong.tistory.com
Contents
1. 파생변수 추가
1.1. 연속형 변수를 범주형 변수로 변환
1.2. 두 변수를 합쳐 파생변수 추가
2. 데이터 분할 및 변수 선택
2.1. 데이터 분할
2.2. 필요 변수 추출
3. 모델 설계 및 학습
3.1. 의사결정나무
3.2. 랜덤 포레스트
1. 파생변수 추가
1-1. 연속형 변수를 범주형 변수로 변환
age 변수는 현재 연속형 변수(numeric)인데, 이것을 범주형 변수(factor)로 바꿔주어 파생변수를 추가해 보도록 하겠다.
본래 연속형 변수를 범주형 변수로 바꾸게 되면 정보의 손실이 발생할 수도 있지만, 파생변수를 추가해보는 과정을 설명하기 위해 진행해보기로 한다.
연속형 변수를 범주형 변수로 변환하는 방법에는 대표적으로 cut(), ifelse(), within() 함수를 사용하는 것이 있다.
개인적으로 이 셋 중에 within() 함수를 가장 자주 사용하는 편이다.
titanic <- within( titanic, {
age_1 = character(0)
age_1[ age <= 16 ] = "A"
age_1[ age >16 & age <= 32 ] = "B"
age_1[ age >32 & age <= 48 ] = "C"
age_1[ age >48 & age <= 64 ] = "D"
age_1[ age >64 ] = "E"
age_1 = factor(age_1, level = c("A", "B", "C", "D", "E"))
})within() 함수는 먼저 새로 만들 변수 age_1 = charactor(0)으로 문자형 변수로 신규 생성 및 지정을 해주고 나서, 수식 등호, 부등호로 구간을 설정해준 후 마지막 줄에 factor() 함수로 level=c("A", "B", "C", "D", "E")로 수준을 지정해준다.
나이는 순서(order)가 있으므로 level에 지정한 순서가 age_1 요인 변수의 level 순서가 된다.
아래는 summary(titanic$age_1)으로 age_1 변수를 살펴본 결과이다.
age 5개 범주 값 별로 탑승객의 수를 확인할 수 있다.
summary(titanic$age_1)
A B C D E
134 787 268 104 13
1-2. 두 변수를 합쳐 파생변수 추가
앞서 살펴본 것처럼 형제, 자매, 배우자, 부모님, 자녀의 수가 많을수록 생존 확률이 높았는데, 두 개의 변수를 합쳐서 Family라는 새로운 파생변수를 추가해보자.
먼저, 파생변수를 추가하기 위해 dplyr 패키지를 설치하고 로드해준다.
dplyr 패키지는 R에서 데이터 전처리를 할 때, 가장 많이 사용되는 패키지 중 하나이다. 데이터의 일부 추출, 새로운 변수 생성, 다른 데이터와 병합 등의 다양한 기능을 지원한다.
dplyr 패키지의 주요 함수들은 아래와 같으며, 이 함수들은 %>%(파이프 연산자 : Ctrl+Shift+M) 기호로 연결하여 중첩 사용이 가능해 데이터를 매우 편리하게 처리하고 분석할 수 있다. 필자도 회사에서 데이터 분석 시 가장 많이 사용하는 패키지이다.
| 함 수 | 기 능 |
| select | 지정한 열 추출 |
| filter | 조건에 맞는 행 추출 |
| mutate | 변수 추가 |
| group_by | 데이터 그룹화 |
| summarise | 요약 통계량 계산 |
| arrange | 데이터 정렬 |
| {left, right, inner, ful}_join | 데이터 병합 |
| bind_{rows, cols} | 행과 열 방향으로 데이터 결합 |
위의 함수들 중에서 파생변수를 추가하기 위해 mutate() 함수를 쓸 것이다.
sibsp와 parch 변수의 합계 값으로 Family라는 새로운 파생변수를 추가해준다.
titanic <- titanic %>% mutate(Family=sibsp+parch)
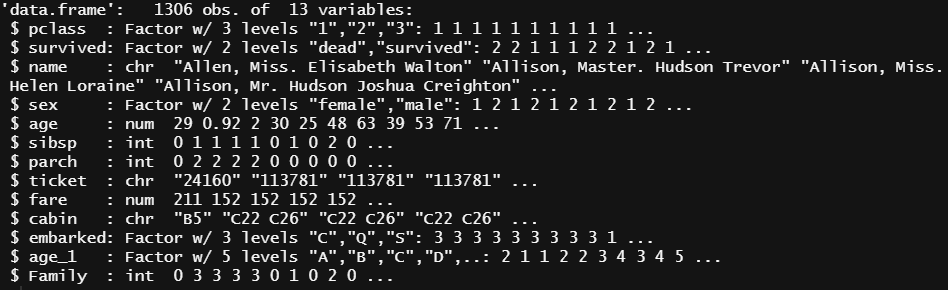
str(titanic)str(titanic)로 데이터 요약을 살펴보면, 제일 아래줄에 Family라는 새로운 파생변수가 추가된 것을 확인할 수 있다.
2. 데이터 분할 및 변수 선택
이제 본격적으로 분류 분석 모델을 구축하기에 앞서, 분류 분석이 무엇인지 간단히 짚고 넘어가도록 하자.
분류 분석은 종속변수의 속성 값에 대해 다양한 변수를 이용하여 모델을 구축하여 새로운 데이터에 대한 예측 및 분류를 수행하는 것으로 , 종속변수가 범주형인 경우 예측 모델은 데이터의 분류가 주목적이며 연속형인 경우는 데이터의 예측이 주목적이다.
고객 콜센터의 경우 조기 퇴사자가 상당히 많아서 퇴사자들의 이력서와 인적성검사 데이터를 기반으로 분류 분석 모델을 구축하고, 그 모델로 신규 지원자의 데이터로 조기 퇴사자의 가능성을 예측하는 용도로 활용하는 사례도 있다고 한다.
우리 회사도 최근 채용 시 AI면접을 도입하였는데, 아마도 거기에는 분류 분석 알고리즘이 사용되지 않았을까 조심스레 예측해본다.
2-1. 데이터 분할
전처리가 완료된 titanic 데이터를 훈련 데이터(train)와 테스트 데이터(test)로 7:3 비율로 분할한다.
아래 코드에서 set.seed(1234)는 난수 생성 시 seed를 지정한 것으로, 데이터 불러들이기부터 테스트 데이터 분할까지의 과정을 혹시라도 여러 번 반복할 일이 있을 때 항상 같은 데이터가 훈련 데이터와 테스트 데이터로 분할되게 하기 위함이다.
만약, seed를 지정하지 않으면 데이터 분리 시마다 매번 다른 데이터가 훈련 데이터로 지정되게 되어 모델링 과정에서 모델 성능이 계속 변하는 등의 혼란이 있을 수 있다.
그다음, sample 함수를 통해 idx 값을 만들어 train과 test 데이터 셋을 70%, 30%로 분할한다. 그러고 나서 train과 test 데이터의 행의 개수를 파악하여 7대 3 비율로 분할이 되었음을 확인한다.
set.seed(1234)
idx<- sample(1:nrow(titanic), size=nrow(titanic)*0.7,replace=FALSE)
train <- titanic[idx,]
test <- titanic[-idx,]
nrow(train)
[1] 914
nrow(test)
[1] 3922-2. 필요 변수 추출
모델링하기 전에 종속변수 survived와 독립변수 pclass, sex, age_1, Family, fare, embarked만 추출하여 train_1과 test_1 데이터를 구축하고 str 함수로 데이터의 구조를 파악해본다.
train_1 <- train[,c("pclass","survived","sex","age_1","fare","embarked","Family")]
test_1 <- test[,c("pclass","survived","sex","age_1","fare","embarked","Family")]
str(test_1)
'data.frame': 392 obs. of 7 variables:
$ pclass : Factor w/ 3 levels "1","2","3": 1 1 1 1 1 1 1 1 1 1 ...
$ survived: Factor w/ 2 levels "dead","survived": 1 1 1 2 2 2 2 1 2 1 ...
$ sex : Factor w/ 2 levels "female","male": 1 1 2 1 1 1 2 2 1 2 ...
$ age_1 : Factor w/ 5 levels "A","B","C","D",..: 1 2 3 4 2 2 5 2 4 3 ...
$ fare : num 151.6 151.6 0 51.5 227.5 ...
$ embarked: Factor w/ 3 levels "C","Q","S": 3 3 3 3 1 3 3 3 1 1 ...
$ Family : int 3 3 0 2 1 0 0 0 1 0 ...3. 모델 설계 및 학습
데이터 분석 전문가(ADP) 18회 차에 출제된 clustering SOM 모델은 오직 숫자형 데이터에만 적용할 수 있기 때문에 titanic 데이터에는 적용할 수 없다. 해당 모델은 다음 포스팅에서 다른 데이터 셋으로 다뤄볼 예정이며, 이번 포스팅에서는 의사결정 나무와 랜덤 포레스트의 모델링과 성과분석에 대하여 알아보겠다.
3-1. 의사결정 나무
1) 모델링
의사결정 나무는 지니 불순도 등의 기준을 사용하여 노드를 재귀적으로 분할하면서 나무 모델을 만드는 방법이다. if-else의 조건문과 같은 형식이어서 이해하기 쉽고 속도가 빠르며, 여러 가지 피처 간의 상호 작용을 잘 표현해주고 다양한 데이터 유형에 사용할 수 있다는 장점이 있다.
install.packages(c("rpart","rpart.plot"))
library(rpart)
library(rpart.plot)
dt.model <- rpart(survived~., #종속변수는 survived, 독립변수는 모든 변수
method="class", # method는 분류인 "class" 선택
data=train_1,
control=rpart.control(maxdepth=4 # 의사결정나무의 최대 깊이는 4개까지
minsplit=15)) # 노드에서 최소 관측치는 15개 이상
dt.model
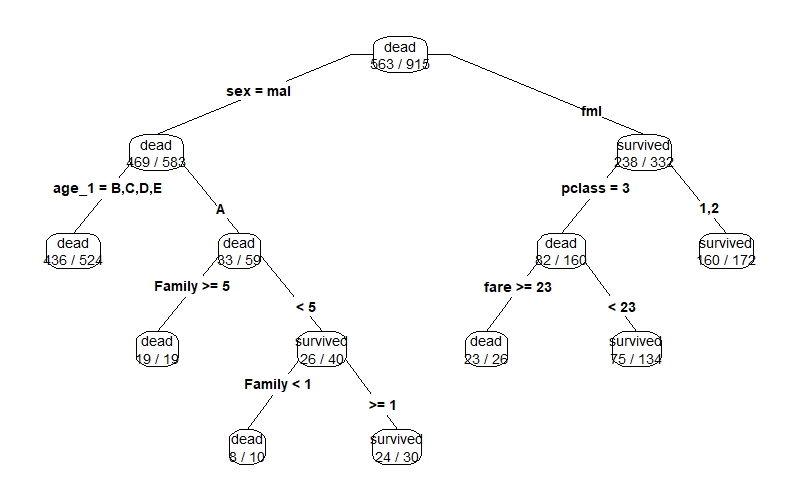
prp(dt.model, type=4, extra=2)아래의 그림을 보면, 총 915명의 승객 중 563명을 사망자(dead)로 분류했으며, 성별이 여자(fml)인 332명 중 238명이 생존자(survived)로 분류되었음을 의미한다. prp 함수는 rpart.plot 패키지에 속한 함수이며, type, extra 등의 인자를 사용하여 그래프 모양을 바꿀 수 있다.
2) 성과분석 : F1-score
다음은 caret 패키지의 confusionMatrix 함수를 사용하여 의사결정 나무 모델 예측을 통한 정 분류율을 확인해보자.
install.packages("caret")
library(caret)
pred.dt <- predict(dt.model, test_1[,-2],type="class")
confusionMatrix(data=pred.dt, reference=test_1[,2],positive='survived')
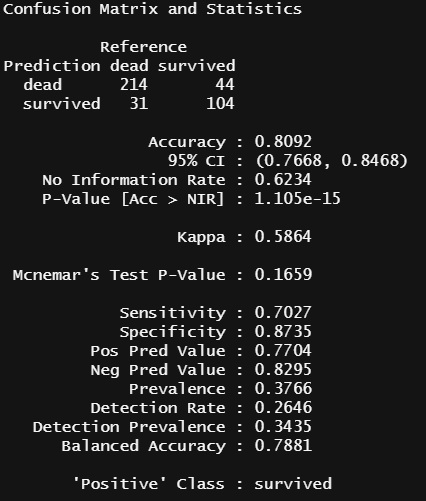
- 정 분류율(Accuracy)은 전체 예측에서(예측이 생존자든 사망자든 무관하게) 옳은 예측의 비율
- 민감도(Sensitivity=Recall)는 실제 생존자(survived)들 중에 예측이 생존자로 된 경우의 비율
- 특이도(Specificity)는 실제 사망자(dead)들 중에 예측이 사망자로 된 경우의 비율
위의 의사결정 나무 모델에서의 정 분류율은 0.8092로 확인되었다.
정 분류율이 높다고 무조건 좋은 모형은 아니며 분석 목적에 따라 다양한 지표들을 고려하여 분석 모형을 선택해야 한다.
다음으로 정확도(precision)와 재현율(recall)을 각각 구하여, F1값을 구해준다.
precision <- posPredValue(pred.dt,test_1[,2], positive="survived")
recall <- sensitivity(pred.dt,test_1[,2], positive="survived")
F1_score <- (2 * precision * recall) / (precision + recall)
precision
[1] 0.7703704
recall
[1] 0.7027027
F1
[1] 0.7349823- 정확도(Presicion) : 생존자로 예측된 승객 중 실제로 생존자인 비율
- 재현율(Recall) : 실제 생존자인 승객 중 예측하여 맞춘 생존자의 비율(= 민감도)
- F1-score : 정확도와 재현율을 보정하여 하나의 지표로 나타낸 값
위의 결과를 보면, F1 값은 0.7350인 것을 확인할 수 있다.
3) 성과분석 : ROC Curve
다음으로 ROC커브를 생성해보자.
install.packages("ROCR")
library(ROCR)
pred.dt.roc<- prediction(as.numeric(pred.dt),as.numeric(test_1[,2]))
plot(performance(pred.dt.roc,"tpr","fpr"))
abline(a=0,b=1,lty=2,col="black")
performance(pred.dt.roc,"auc")@y.values
[[1]]
[1] 0.788086ROCR 패키지의 ROCR 함수를 활용하여 ROC 커브를 그린다. 의사결정 나무 분석 결과의 AUC값은 0.7881(78.81%)로 모델의 성능은 보통 수준으로 나타난다.

3-2. 랜덤 포레스트(Random Forest)
1) 모델링
랜덤 포레스트 모델은 의사결정나무의 단점인 분산이 크다는 점을 고려하여 더 많은 무작위성을 주어 약한 학습기들을 생성한 후 이를 선형 결합하여 최종 학습기를 만드는 방법이다. randomForest 패키지로 구현이 가능하다.
install.packages("randomForest")
library(randomForest)
rf.model <- randomForest(survived~.,data=train_1)
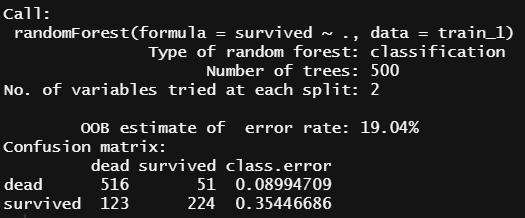
print(rf.model)랜덤 포레스트 분석결과에서 "OOB estimate of error rate"의 값은 에러 추정치로서 값이 낮을수록 분류모델 성능이 좋다고 할 수 있는데, 생성된 모델을 보면 OOB가 약 19%로 분류모델의 성능이 썩 좋게 나타나진 않고 있으며, Confusion Matrix의 class.error값이 survived일 때 약 0.35로 높게 나타나 있음을 알 수 있다.
여기서 0.35가 의미하는 것은, 생성된 랜덤포레스트 모델이 실제 titanic의 생존자 347명 중에 약 35.4%인 123명을 사망자로 오분류한다는 것이다.
2) 성과분석 : F1-score
pred.rf <- predict(rf.model,test_1[,-2],type="class")
confusionMatrix(data=pred.rf, reference=test_1[,2],positive="survived")
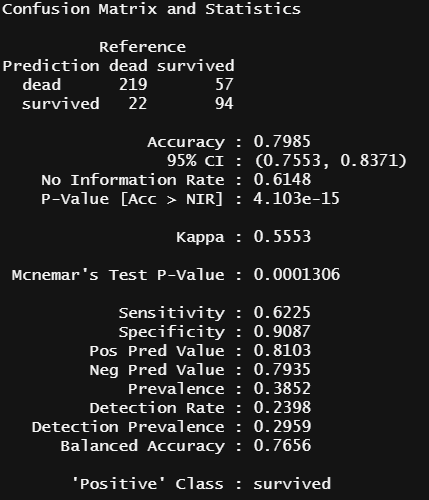
랜덤 포레스트 모델에서의 정 분류율은 0.7985로 의사결정 나무의 정확도보다는 다소 낮게 나타났다.
앞에서 정 분류율이 높다고 무조건 좋은 모형은 아니며 분석 목적에 따라 다양한 지표들을 고려하여 분석 모형을 선택해야 한다고 했는데, 이것을 예를 들어 설명하자면 이렇다.
암환자를 검사하여 분류하는 모델이 있다고 가정하면, 정 분류율(Accuracy)는 이 모델이 암환자든 아니든 옳게 예측한 비율이고 실제 암환자를 암환자로 예측하는 비율이 민감도(Sensirivity)이고 실제 건강한 사람을 암환자가 아니라고 예측하는 비율이 특이도(Specificity)이다.
과연 이 세 가지 지표 중 어떤 지표가 현실에서 가장 중요한 성과지표가 될 수 있을까?
암환자를 건강하다고 판단하는 경우가 가장 치명적일 것이다. 왜냐하면 치료시기를 놓쳐 생명이 위험해질 수도 있기 때문이다. 이런 경우가 민감도가 중요한 성과지표가 된다고 할 수 있겠다.
다음으로 정확도(precision)와 재현율(recall)을 각각 구하여, F1값을 구해준다.
precision <- posPredValue(pred.rf,test_1[,2], positive="survived")
recall <- sensitivity(pred.rf,test_1[,2], positive="survived")
F1 <- (2 * precision * recall) / (precision + recall)
precision
[1] 0.8103448
recall
[1] 0.6225166
F1
[1] 0.7041199위의 결과를 보면, F1 값은 0.7041로 의사결정나무 모델보다 낮은 것을 알 수 있다.
3) 성과분석 : ROC Curve
pred.rf.roc<- prediction(as.numeric(pred.rf),as.numeric(test_1[,2]))
plot(performance(pred.rf.roc,"tpr","fpr"))
abline(a=0,b=1,lty=2,col="black")
performance(pred.rf.roc,"auc")@y.values
[[1]]
[1] 0.7656151ROCR 패키지의 ROCR 함수를 활용하여 ROC 커브를 그려보면, 랜덤 포레스트 분류 분석 결과의 AUC값은 0.7656(76.56%)으로 모델의 성능이 의사결정 나무 모델보다 낮게 나타난다.
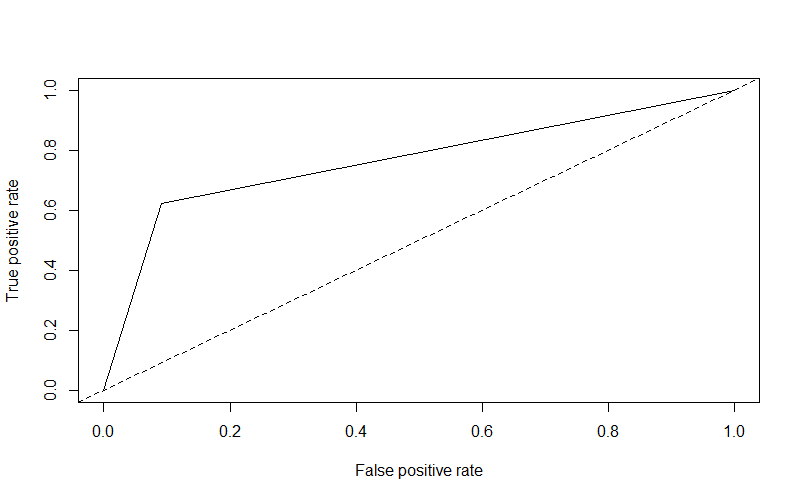
지금까지 분류 분석을 할 수 있는 기계 학습의 모델링과 성과분석에 관해 알아보았다.
두 모델의 성과를 비교해보면, 의사결정 나무의 분석결과가 정분류율은 약 81%로 랜덤포레스트보다 2%정도 높게 나타나고, F1-score, AUC 값에서도 의사결정나무 모델의 성능이 좋게 나타났다.
분류 분석을 위한 기계학습 알고리즘을 만들 때는 항상 데이터의 특성에 따라 성과지표를 잘 파악하여 해당 데이터에 가장 적절한 분석 모형을 선택해야 한다.
'Work > ADP' 카테고리의 다른 글
| [ADP 실기 준비] R 통계분석 / 선형회귀분석 / 변수선택법 (2) | 2020.11.16 |
|---|---|
| [ADP 실기 준비] R 기계 학습 - 인공신경망 (4) | 2020.11.11 |
| [ADP 실기 준비] R프로그래밍 기계 학습 - 탐색적 자료분석(EDA) (2) | 2020.10.28 |
| [ADP 실기 준비] R 프로그래밍 기계 학습 - 데이터 전처리 (8) | 2020.10.21 |
| [ADP 실기 준비] R 시계열 분석 2탄 / ARIMA 모델 / 기출공략 (0) | 2020.10.14 |




댓글