[ADP 실기 준비] R 통계분석 / 선형 회귀분석 / 변수 선택법
통계분석은 ADP 실기 시험에서 꾸준히 출제되고 있는 문제 유형으로서 가장 기본적인 스타일의 문제부터 최근 출제된 경향까지 단계적으로 학습해보려 한다.
이번 포스팅에서는 통계분석 중 선형 회귀분석과 변수 선택법에 관해 알아보자.
Contents
1. 각 설명변수들과 종속변수 간의 상관관계 분석
2. 상관분석 시각화
3. 변수 선택법을 활용한 회귀모형 생성
1. 각 설명변수들과 종속변수 간 상관관계 분석
우선 학습할 데이터는 R 프로그램의 ISLR 패키지에 있는 Carseats 데이터를 사용한다. 이 데이터는 자동차 좌석에 대한 판매정보이며, 변수의 설명은 아래와 같다.
| 변수 | 데이터 형태 | 설명 |
| Sales | 수치형 | 각 지역의 매출 (단위 : 천 달러) |
| CompPrice | 수치형 | 각 위치에서 경쟁업체가 부과하는 가격 |
| Income | 수치형 | 지역 소득 수준 |
| Advertising | 수치형 | 각 지역의 광고 예산 |
| Population | 수치형 | 지역 인구 (단위 : 천 명) |
| Price | 수치형 | 자동차 좌석의 가격 |
| ShelveLoc | 범주형 | 보관 장소의 품질 (Bad, Medium, Good) |
| Age | 수치형 | 인구 연령대 |
| Education | 수치형 | 지역의 교육 수준 |
| Urban | 범주형 | 도시인지 여부 (Yes, No) |
| US | 범주형 | 미국인지 여부 (Yes, No) |
우선, R의 내장 데이터 Carseats를 읽어온 뒤, 데이터의 구조와 요약을 확인해보자.
install.packages("ISLR")
library(ISLR)
data("Carseats")
car<-Carseats
str(car) #데이터 구조
head(car) #데이터 요약
sum(is.na(car)) #결측치(NA)가 존재하는지 확인
[1] 0
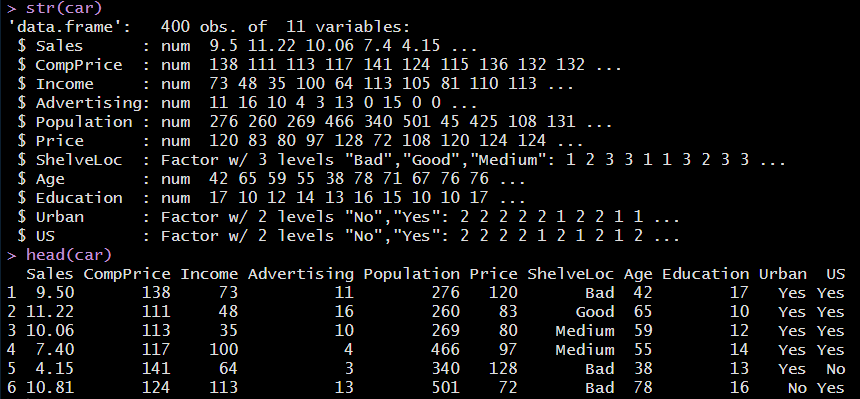
이제 종속변수인 Sales 변수와 CompPrice, Income, Advertising, Population, Price, Age, Education 수치형 변수들 간에 피어슨 상관계수를 이용하여 상관관계 분석을 진행한다.
1-1. Sales와 CompPrice 간의 상관분석
cor(car$Sales,car$CompPrice) # 피어슨 상관계수 산출
cor.test(car$Sales,car$CompPrice) # 피어슨 상관계수 검정

해석
상관계수는 약 0.064로 Sales와 CompPrice 간에는 거의 상관성이 존재하지 않는다고 볼 수 있다.
p-value가 0.2009로 0.05보다 크기 때문에, 두 변수 간의 상관관계는 통계적으로 유의하다고 볼 수 없다.
1-2. Sales와 Income 간의 상관분석
cor(car$Sales,car$Income)
cor.test(car$Sales,car$Income)

해석
p-value는 0.05보다 작으므로 두 변수간의 상관관계는 통계적으로는 유의하나, 상관계수는 약 0.15로 Sales와 Income 간에는 상관관계가 거의 없다고 볼 수 있다.
1-3. Sales와 Advertising 간의 상관분석
cor(car$Sales,car$Advertising)
cor.test(car$Sales,car$Advertising)

해석
p-value는 0.05보다 작으므로 두 변수간의 상관관계는 통계적으로는 유의하나, 상관계수는 약 0.27로 Sales와 Advertising 간에는 상관관계가 거의 없다고 볼 수 있다.
1-4. Sales와 Population 간의 상관분석
cor(car$Sales,car$Population)
cor.test(car$Sales,car$Population)

해석
상관계수는 약 0.05로 Sales와 Population 간에는 거의 상관성이 존재하지 않는다고 볼 수 있다.
p-value가 0.314로 0.05보다 크기 때문에, 두 변수간의 상관관계는 통계적으로 유의하다고 볼 수 없다.
1-5. Sales와 Price 간의 상관분석
cor(car$Sales,car$Price)
cor.test(car$Sales,car$Price)

해석
p-value는 0.05보다 작으므로 두 변수간의 상관관계는 통계적으로는 유의하다.
또한 상관계수는 약 -0.445로 Sales와 Price 간에는 다소 약한 음의 상관관계를 가지고 있다.
1-6. Sales와 Age 간의 상관분석
cor(car$Sales,car$Age)
cor.test(car$Sales,car$Age)
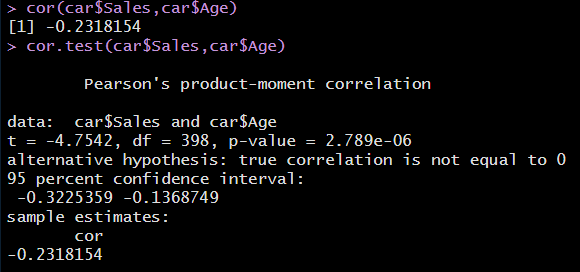
해석
p-value는 0.05보다 작으므로 두 변수간의 상관관계는 통계적으로는 유의하다.
상관계수는 약 -0.232로 상관계수의 절댓값이 0.5보다 작기 때문에 Sales와 Age 간에는 상관관계가 거의 없다고 볼 수 있다.
1-7. Sales와 Education 간의 상관분석
cor(car$Sales,car$Education)
cor.test(car$Sales,car$Education)

해석
상관계수는 약 -0.052로 Sales와 Education 간에는 거의 상관성이 존재하지 않는다고 볼 수 있다.
p-value가 0.2999로 0.05보다 크기 때문에, 두 변수 간의 상관관계는 통계적으로 유의하다고 볼 수 없다.
2. 상관분석 시각화
다음으로, 상관분석을 수행했던 변수들에 대해 상관계수 행렬을 생성하고 이를 시각화한다.
cor(car[,-c(7,10,11)])
plot(car[,-c(7,10,11)])


해석
앞서 상관분석 결과를 살펴보면, 종속변수인 Sales와 통계적으로 유의한 상관성을 가지는 변수는 Income, Advertising, Price, Age이다. 하지만 상관관계 산점도 그래프를 보면, 대부분의 변수들이 일정한 직선의 형태가 아닌 산발적으로 분포된 것을 확인할 수 있다. Sales 변수와 Price 변수 간의 상관계수의 절대값이 약 0.44로 가장 크다. 이는 일반적으로는 높은 상관성을 지닌다고 볼 수 없는 수치지만, 산점도를 봤을 때 두 변수간의 데이터는 다른 데이터들에 비해 비교적 상관성을 띠며 왼쪽 위에서 아래로 내려가는 형태를 보이고 있다. 이는 두 변수 간에 미미하지만 음의 상관관계를 가진다고 해석할 수 있다.
3. 변수 선택법을 활용한 회귀모형 생성
선형 회귀 모델을 만들 때, 주어진 여러 변수 중 어떤 ㅂ면수를 설명 변수로 해야 할지는 모델링을 수행하는 사람의 배경 지식에 따라 결정할 수 있다. 하지만 배경 지식이 없거나, 배경 지식이 있어도 어떤 변수들을 선택해야 할지 정확히 결정할 수 없다면, 변수의 통계적 특성을 고려하여 기계적으로 설명 변수를 채택하는 방법을 사용할 수 있다.
회귀 모델에서의 설명 변수를 선택하는 방법 중 한 가지는 AIC 기준을 사용해 변수를 하나씩 택하거나 제거하는 것이다.
이번 학습에서는 후진 제거법을 사용하여 회귀분석을 실시하고, 추정된 회귀모형을 생성해보자.
step(lm(Sales~CompPrice+Income+Advertising+Population+Price+Age+Education
,data=car), direction="backward")

해석
후진 제거법의 첫 번째 단계를 확인해보면 Population 변수가 모형에서 제거되었을 때, AIC값이 531.53으로 가장 작으므로 Population 변수가 모형에서 제거됨을 알 수 있다.
두 번째 단계에서는 Education 변수가 제거되었을 때, AIC값이 가장 작아지기 때문에 Education 변수가 모형에서 제거된다.
위와 같은 변수 제거 과정을 거쳐 lm(formula = Sales ~ CompPrice + Income + Advertising + Price + Age, data=car)라는 최종 회귀 모형이 결정되었다.
최종적으로 선택된 추정 회귀식은 y = 7.110919 + 0.09390*CompPrice + 0.01309*Income - 0.09254*Price - 0.04497*Age이다.
앞서 진행한 후진 제거법을 통해 선택된 변수들로 새로운 회귀모형을 생성해보자.
car.lm <- lm(Sales ~ CompPrice + Income + Advertising + Price + Age, data = car)
summary(car.lm)
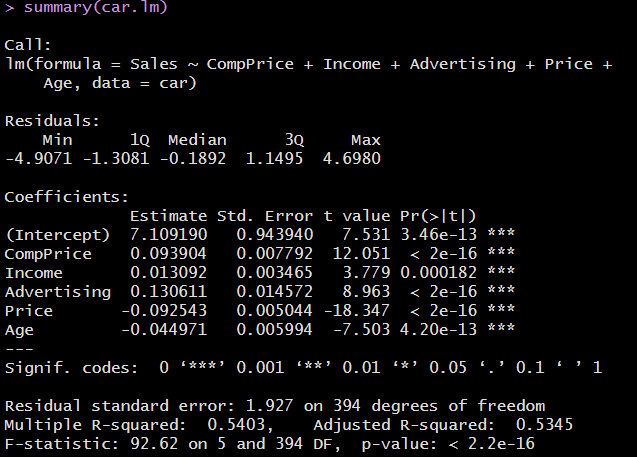
해석
후진제거법을 이용한 변수 선택 후, 선택된 변수들로 회귀분석을 수행한 결과, 모든 변수들의 유의 확률이 0.05보다 작아 통계적으로 유의함을 확인할 수 있다. 하지만 모형의 결정계수가 0.5403, 수정된 결정계수는 0.5345로 추정된 다변량 회귀식은 전체 데이터의 변동을 약 53% 설명하고 있어 다소 낮은 설명력을 가진다고 보인다.
회귀모형의 F통계량에 대한 p-calue값은 0.05보다 작으므로 유의 수준 0.05하에서 모형은 통계적으로 유의한 것을 알 수 있다.
회귀분석 결과로 추정된 최종 회귀식은 y = 7.110919 + 0.09390*CompPrice + 0.01309*Income - 0.09254*Price - 0.04497*Age이다.
지금까지 R을 활용한 선형 회귀분석에 관하여 알아보았다.
'Work > ADP' 카테고리의 다른 글
| [ADP 실기 준비] R 기계 학습 - 인공신경망 (4) | 2020.11.11 |
|---|---|
| [ADP 실기 준비] R 기계 학습 - 분류분석 모델링 및 성과 분석 (6) | 2020.10.30 |
| [ADP 실기 준비] R프로그래밍 기계 학습 - 탐색적 자료분석(EDA) (2) | 2020.10.28 |
| [ADP 실기 준비] R 프로그래밍 기계 학습 - 데이터 전처리 (8) | 2020.10.21 |
| [ADP 실기 준비] R 시계열 분석 2탄 / ARIMA 모델 / 기출공략 (0) | 2020.10.14 |




댓글